In the realm of geometry and trigonometry, the concept of an arc chord calculator plays a crucial role in simplifying complex calculations. This powerful tool allows users to determine various properties of arcs and chords in circles, making it indispensable for students, architects, engineers, and anyone involved in design and construction. Understanding how to effectively use an arc chord calculator can enhance your ability to solve real-world problems related to circular shapes.
The arc chord calculator not only saves time but also improves accuracy in calculations that would otherwise require tedious manual work. By inputting specific parameters, users can obtain valuable information such as the length of the chord, the radius of the circle, and the angle subtended by the arc. This article will delve into the functionality of arc chord calculators, how to use them, and the mathematical concepts behind them.
Throughout this comprehensive guide, we will explore the importance of mastering the arc chord calculator, its applications across various fields, and the underlying principles that govern its use. Whether you're a student looking to improve your math skills or a professional seeking to streamline your workflow, this article is designed to provide you with essential insights and practical knowledge.
Table of Contents
- Understanding Arc and Chord
- Importance of Arc Chord Calculator
- How Arc Chord Calculator Works
- Key Formulas Used
- Applications in Real World
- Step-by-Step Guide to Use
- Common Mistakes to Avoid
- Frequently Asked Questions
Understanding Arc and Chord
To effectively use an arc chord calculator, it's essential to grasp the fundamental concepts of arcs and chords. An arc is a segment of a circle's circumference, while a chord is a straight line connecting two points on the circle. Understanding the relationship between these two elements is key to performing calculations accurately.
Definition of Arc
An arc is defined as a portion of the perimeter of a circle. The length of an arc can be calculated based on the angle subtended at the center of the circle and the radius. For instance, if the radius of a circle is known, the length of the arc can be determined using the formula:
Arc Length = (θ/360) * 2πr
where θ is the angle in degrees and r is the radius.
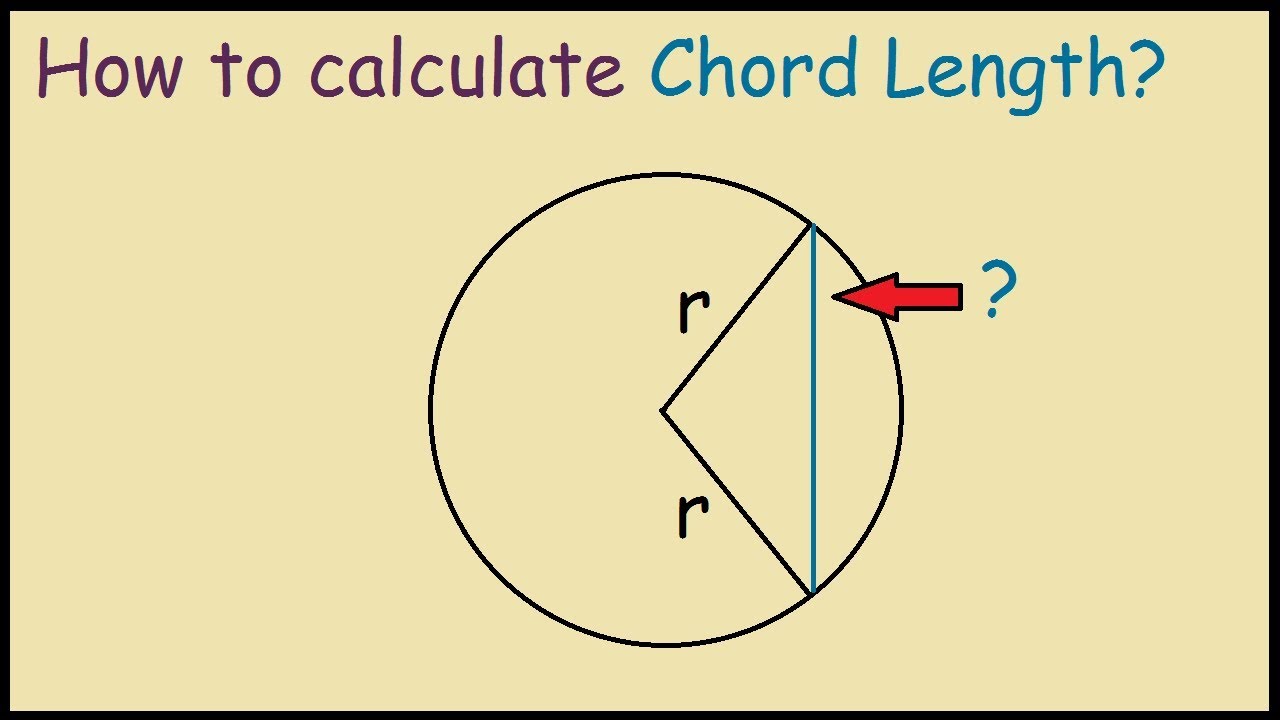
Definition of Chord
A chord is a line segment whose endpoints lie on the circle. The length of the chord can be derived using the radius and the angle subtended by the chord at the center of the circle. The formula for the length of the chord is:
Chord Length = 2r * sin(θ/2)
where r is the radius and θ is the angle in degrees.
Importance of Arc Chord Calculator
The arc chord calculator is an invaluable tool for anyone working with circular geometries. Its importance can be summarized in several key points:
- Efficiency: Speeds up calculations that would otherwise be time-consuming.
- Accuracy: Minimizes human error in mathematical computations.
- User-Friendly: Accessible to individuals with varying levels of mathematical expertise.
- Versatile: Applicable in various fields including engineering, architecture, and design.
How Arc Chord Calculator Works
Arc chord calculators function by taking specific inputs, such as the radius of the circle and the angle subtended by the arc. The calculator then processes these inputs to provide outputs, including the length of the arc, the length of the chord, and other related measurements. Most online calculators are straightforward, requiring users to simply input the necessary values and click a button to receive results.
Key Formulas Used
Understanding the key formulas used in arc and chord calculations is crucial for effective use of the calculator. Below are the most commonly used formulas:
- Arc Length:
Arc Length = (θ/360) * 2πr - Chord Length:
Chord Length = 2r * sin(θ/2) - Radius from Chord and Arc:
r = (Chord Length²)/(8 * Arc Height) + (Arc Height/2)
Applications in Real World
The applications of arc chord calculations extend to multiple fields:
- Engineering: Used in structural design to ensure stability and accuracy in circular components.
- Architecture: Essential in designing arches and rounded structures.
- Aerospace: Critical for calculations involving flight paths and circular trajectories.
- Manufacturing: Applied in the production of circular objects and components.
Step-by-Step Guide to Use Arc Chord Calculator
Here is a simple guide on how to use an arc chord calculator effectively:
- Identify the parameters: Determine the radius of the circle and the angle subtended by the arc.
- Input the values: Enter the radius and angle into the calculator.
- Click calculate: Press the calculate button to get results.
- Review results: Examine the output for the length of the arc, chord, and any other relevant measurements.
Common Mistakes to Avoid
While using an arc chord calculator, it's important to avoid common pitfalls that can lead to inaccurate results:
- Incorrect units: Ensure all measurements are in the same unit (e.g., meters, centimeters).
- Misinterpreting angle: Confirm that angles are in degrees or radians as required by the calculator.
- Forgetting to check results: Always verify that the output makes sense logically.
Frequently Asked Questions
Here are answers to some common questions regarding arc chord calculators:
- What is the difference between an arc and a chord? An arc is a part of the circle's circumference, while a chord is a straight line connecting two points on the circle.
- Can I use an arc chord calculator for any circle? Yes, as long as you have the radius and angle, the calculator can be used for any circle.
- Is there a cost associated with using an online arc chord calculator? Most online calculators are free to use, making them accessible to everyone.
Conclusion
In conclusion, the arc chord calculator is a powerful tool that simplifies the process of calculating lengths and dimensions associated with arcs and chords. By understanding the fundamental concepts, applying the key formulas, and following a step-by-step guide, users can harness the full potential of this calculator. We encourage readers to explore further, engage with the content, and share their experiences or questions in the comments below.
Call to Action
Don't hesitate to put your newfound knowledge into practice! Whether you're a student or a professional, utilizing the arc chord calculator can greatly enhance your efficiency and accuracy. Share this article with others who may benefit, and explore more content on our site to expand your understanding of geometry and its applications.
Final Thoughts
We hope you found this guide informative and helpful. Remember, mastering the arc chord calculator is a valuable skill that can aid you in various fields. We look forward to seeing you again on our site for more insights and resources!
Article Recommendations
- Sykkuno Net Worth 2023 Estimated Earnings Income
- Jonas Armstrong Wife Insights Into His Personal Life And Relationships
- Insights On Cindy Williams And Bill Hudson Their Lives And Careers