The tangent function, commonly abbreviated as "tan," is a fundamental concept in trigonometry that plays a crucial role in various fields such as mathematics, physics, and engineering. Understanding the range of tan is essential for students and professionals alike, as it aids in solving problems related to angles and triangles. In this article, we will explore the range of the tangent function, its properties, and its applications. We will also delve into the mathematical principles that govern this intriguing function, providing you with a comprehensive understanding.
The tangent function is defined as the ratio of the opposite side to the adjacent side in a right triangle. However, its behavior is not restricted to just triangles; it extends to the unit circle and has implications in complex mathematics. In this article, we will break down the details of the tan function, including its range, domain, and how to effectively use it in various mathematical contexts.
By the end of this article, you will not only understand what the range of tan is, but also how to apply this knowledge in practical scenarios. So, let’s dive deeper into the fascinating world of trigonometry and discover the range of the tangent function.
Table of Contents
- What is the Tangent Function?
- Mathematical Definition of Tangent
- Range of Tan Function
- Domain of Tan Function
- Graph of the Tangent Function
- Applications of the Tangent Function
- Common Misconceptions about Tan
- Conclusion
What is the Tangent Function?
The tangent function is one of the primary trigonometric functions, alongside sine and cosine. It is typically defined for an angle θ in a right triangle as follows:
- Tan(θ) = Opposite / Adjacent
In the context of the unit circle, the tangent function represents the length of the segment from the point on the unit circle to the x-axis, extending vertically. This geometric interpretation provides valuable insights into the behavior of the tan function.
Mathematical Definition of Tangent
Mathematically, the tangent function can be expressed using sine and cosine as:
- Tan(θ) = Sin(θ) / Cos(θ)
Because of this definition, the tangent function is undefined whenever the cosine of the angle is zero, which occurs at odd multiples of π/2 (90°, 270°, etc.).
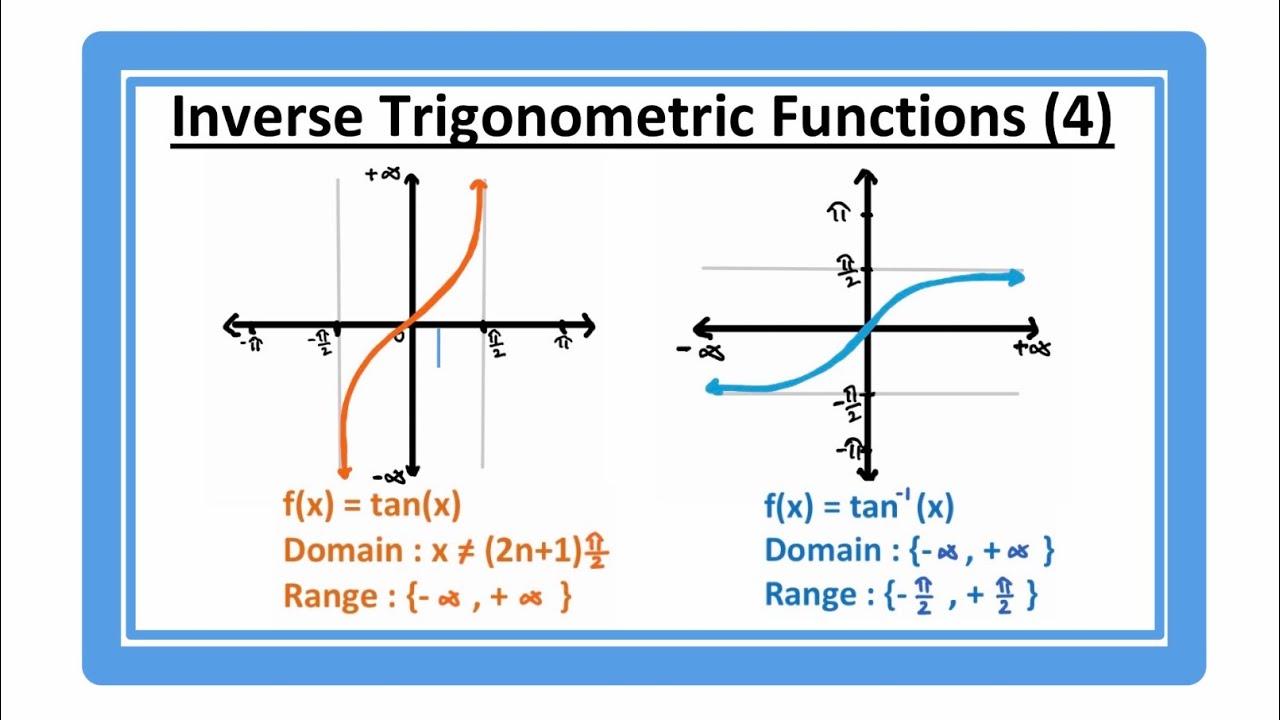
Range of Tan Function
Now, let’s focus on the range of the tangent function. The range of tan is all real numbers, which can be mathematically expressed as:
- Range: (-∞, +∞)
This means that for any real number output, there exists an angle θ such that tan(θ) equals that output. This is a unique and important feature of the tangent function, distinguishing it from other trigonometric functions like sine and cosine, which have limited ranges.
Domain of Tan Function
In contrast to its range, the domain of the tangent function is limited. The domain of tan is all real numbers except for odd multiples of π/2, where the function is undefined:
- Domain: x ∈ ℝ, x ≠ (2n + 1)π/2 for any integer n
This restriction occurs because at these angles, the cosine function equals zero, resulting in division by zero in the tangent formula.
Graph of the Tangent Function
The graph of the tangent function exhibits a periodic behavior with a period of π, meaning the function repeats every π units. It possesses vertical asymptotes at points where the function is undefined, creating a unique wave-like pattern. Below are some key points regarding the graph:
- The graph crosses the origin (0,0).
- As it approaches the asymptotes, the function tends to ±∞.
- The function oscillates between the asymptotes, covering all real numbers.
Visualizing the graph can greatly enhance your understanding of the range and behavior of the tangent function.
Applications of the Tangent Function
The tangent function has numerous applications across various fields, including:
- Engineering: Used in calculations involving angles and slopes.
- Physics: Utilized in analyzing forces and motion.
- Architecture: Essential in determining structural angles and stability.
Understanding the range of tan is vital for effective problem-solving in these disciplines.
Common Misconceptions about Tan
Despite its widespread use, there are several common misconceptions regarding the tangent function:
- Some believe that tan can only take values between -1 and 1, which is incorrect.
- Others may confuse the range of tan with that of sine and cosine, which are limited.
Clarifying these misconceptions is essential for a proper understanding of trigonometric functions.
Conclusion
In summary, the tangent function is a powerful tool in trigonometry with a range that encompasses all real numbers. Understanding its properties, including the range and domain, is crucial for anyone studying mathematics or related fields. We encourage you to explore further, practice problems involving the tangent function, and engage with others to solidify your understanding.
If you have any questions or comments about the tangent function, please feel free to leave them below. Don’t forget to share this article with others who might find it useful!
Thank you for reading, and we look forward to seeing you back on our site for more informative articles!
Article Recommendations
- Unveiling The Life And Times Of Camryn Manheim Love Life And Legacy
- Who Is Karen Taylor Meet Travis Taylors Wife
- Playboi Carti Gun A Deep Dive Into The Controversial Icon