Graphing tangent functions is an essential skill in mathematics, particularly in the study of trigonometry. Understanding how to graph these functions not only enhances your mathematical abilities but also provides practical applications in various fields, including physics, engineering, and computer science. In this article, we will delve deep into the intricacies of graphing tangent functions, explore their properties, and provide you with all the tools you need to master this topic.
By the end of this article, you will have a comprehensive understanding of graphing tangent functions, and you will be equipped with valuable resources and insights to further enhance your learning. Let's dive into the world of trigonometric functions and unlock the mysteries behind the tangent function!
Table of Contents
- Introduction to Tangent Functions
- Properties of Tangent Functions
- How to Graph Tangent Functions
- Understanding Asymptotes
- Transformations of Tangent Functions
- Applications of Tangent Functions
- Examples of Graphing Tangent Functions
- Conclusion
Introduction to Tangent Functions
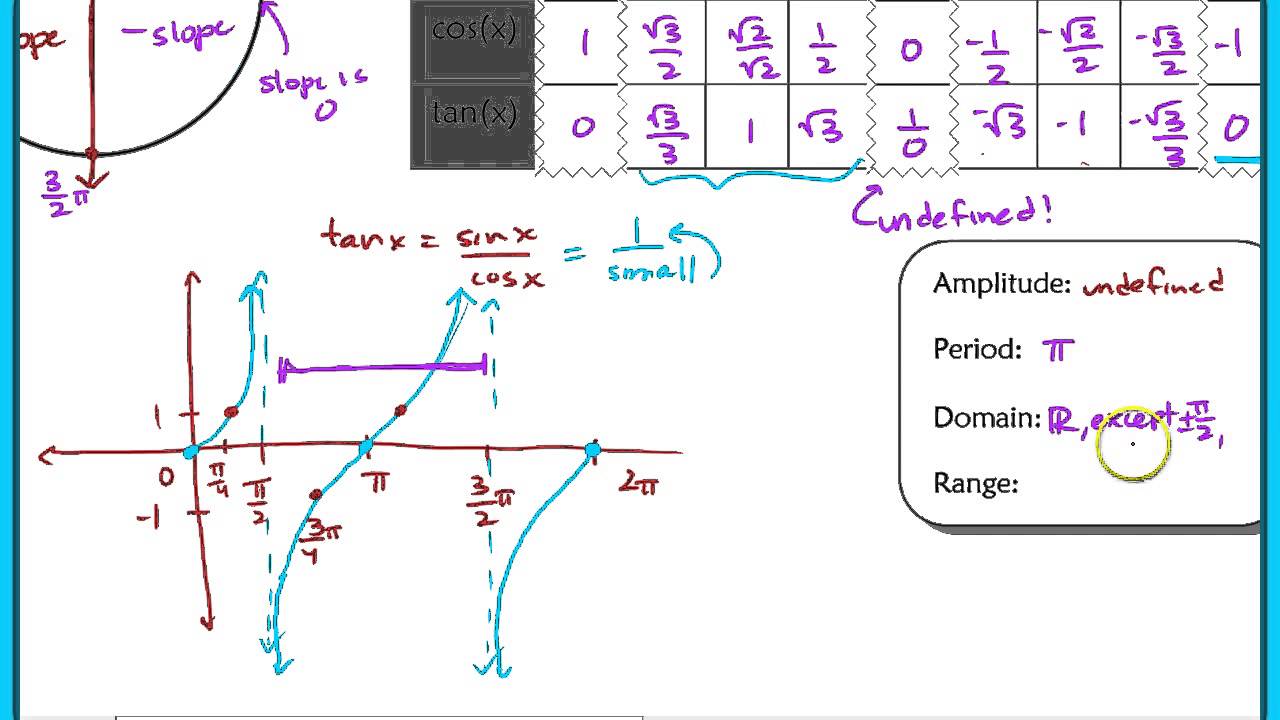
The tangent function is one of the fundamental trigonometric functions, defined as the ratio of the sine and cosine functions. Mathematically, it can be expressed as:
tan(θ) = sin(θ) / cos(θ)
With this definition, we can see that tangent functions exhibit unique characteristics, including periodicity and asymptotic behavior. The tangent function is periodic with a period of π, meaning that its values repeat every π units along the x-axis. This periodicity is one of the key features that make graphing tangent functions an intriguing endeavor.
Properties of Tangent Functions
To graph tangent functions effectively, it is crucial to understand their properties. Here are some key properties:
- Periodicity: The tangent function has a period of π, meaning it repeats every π radians.
- Asymptotes: Vertical asymptotes occur at odd multiples of π/2, where the tangent function is undefined.
- Range: The range of the tangent function is all real numbers (-∞, ∞).
- Symmetry: The tangent function is an odd function, meaning that tan(-θ) = -tan(θ).
How to Graph Tangent Functions
Graphing tangent functions involves several key steps:
Step 1: Identify Key Points
Identify key points within one period of the tangent function. The most common points to consider are:
- tan(0) = 0
- tan(π/4) = 1
- tan(π/2) is undefined (asymptote)
- tan(3π/4) = -1
- tan(π) = 0
Step 2: Plot the Asymptotes
Since the tangent function has vertical asymptotes, it is crucial to plot these lines on the graph. The asymptotes occur at:
- x = π/2 + nπ, where n is an integer (±1, ±2, ...)
Step 3: Sketch the Graph
Using the identified key points and asymptotes, sketch the curve of the tangent function. The graph will approach the asymptotes but never touch them, creating the characteristic "S" shape of the tangent function.
Understanding Asymptotes
Asymptotes play a significant role in the graphing of tangent functions. Let's delve deeper into their importance:
- Location: Vertical asymptotes occur at x = π/2 + nπ, indicating where the function is undefined.
- Behavior: As the function approaches the asymptote from the left, the values tend to -∞, while they tend to +∞ from the right.
Transformations of Tangent Functions
Transformations can change the standard tangent function into various forms. The general form is:
y = a * tan(b(x - c)) + d
- Vertical Stretch/Compression (a): Affects the steepness of the graph.
- Horizontal Stretch/Compression (b): Affects the period; the period is π/b.
- Horizontal Shift (c): Moves the graph left or right.
- Vertical Shift (d): Moves the graph up or down.
Applications of Tangent Functions
Tangent functions have various applications in real-world scenarios, including:
- Physics: Analyzing wave patterns and oscillations.
- Engineering: Designing structures and understanding angles of elevation and depression.
- Computer Graphics: Rendering curves and surfaces in 3D modeling.
Examples of Graphing Tangent Functions
To solidify your understanding, let's look at some examples:
Example 1: Graphing y = tan(x)
Plot the key points, asymptotes, and sketch the graph for one period. The graph will repeat every π units.
Example 2: Graphing y = 2 * tan(x - π/4)
This transformation stretches the graph vertically by a factor of 2 and shifts it to the right by π/4. Identify the new key points and asymptotes before sketching.
Conclusion
In conclusion, graphing tangent functions requires a solid understanding of their properties and behavior. By mastering the key steps outlined in this article, you can confidently graph tangent functions in various forms. We encourage you to practice graphing different tangent functions and explore their applications in real life.
If you found this article helpful, please leave a comment, share it with others, or explore more articles on our site to enhance your mathematical knowledge.
References
- Stewart, James. "Calculus: Early Transcendentals". Cengage Learning.
- Webster, William. "Understanding the Tangent Function". Journal of Mathematics Education.
- OpenStax. "Precalculus". OpenStax College.
Article Recommendations
- The Allencompassing Guide To The November 18th Zodiac Sign
- Eleanor Mitch Mcconnell A Family Legacy
- Colt Knost Career Earnings Top Moneymaking Highlights

![Graphing Tangent Functions Using Transformations • [5.3b] PRECALCULUS](https://i.ytimg.com/vi/lHCtm1O7Jsk/maxresdefault.jpg)