Finding the distance from a point to a line is a fundamental concept in geometry and analytic mathematics. This topic is not only essential for students but also applicable in various fields such as engineering, physics, and computer science. Understanding how to calculate this distance can aid in solving real-world problems, making it a valuable skill to possess.
In this article, we will explore the mathematical principles behind finding the distance from a point to a line. We will discuss various methods and formulas used to achieve this, along with practical examples to illustrate the concepts. By the end of this article, you will have a comprehensive understanding of how to effectively calculate distances in a two-dimensional space.
Whether you are a student preparing for an exam or a professional looking to enhance your skills, this guide will provide you with the necessary knowledge to confidently approach problems related to distances between points and lines. Let’s dive into the details!
Table of Contents
- Understanding Basic Concepts
- Mathematical Representation of a Line
- Distance Formula from a Point to a Line
- Practical Examples
- Applications in the Real World
- Common Mistakes in Calculating Distance
- Advanced Topics in Geometry
- Conclusion
Understanding Basic Concepts
Before diving into the calculations, it's crucial to understand the basic concepts of points and lines in geometry. A point represents a specific location in a two-dimensional space, while a line is defined as a straight path that extends infinitely in both directions. The distance between a point and a line is the shortest path from the point to the line, which is always perpendicular to the line.
Mathematical Representation of a Line
A line in a two-dimensional Cartesian coordinate system can be represented using the equation:
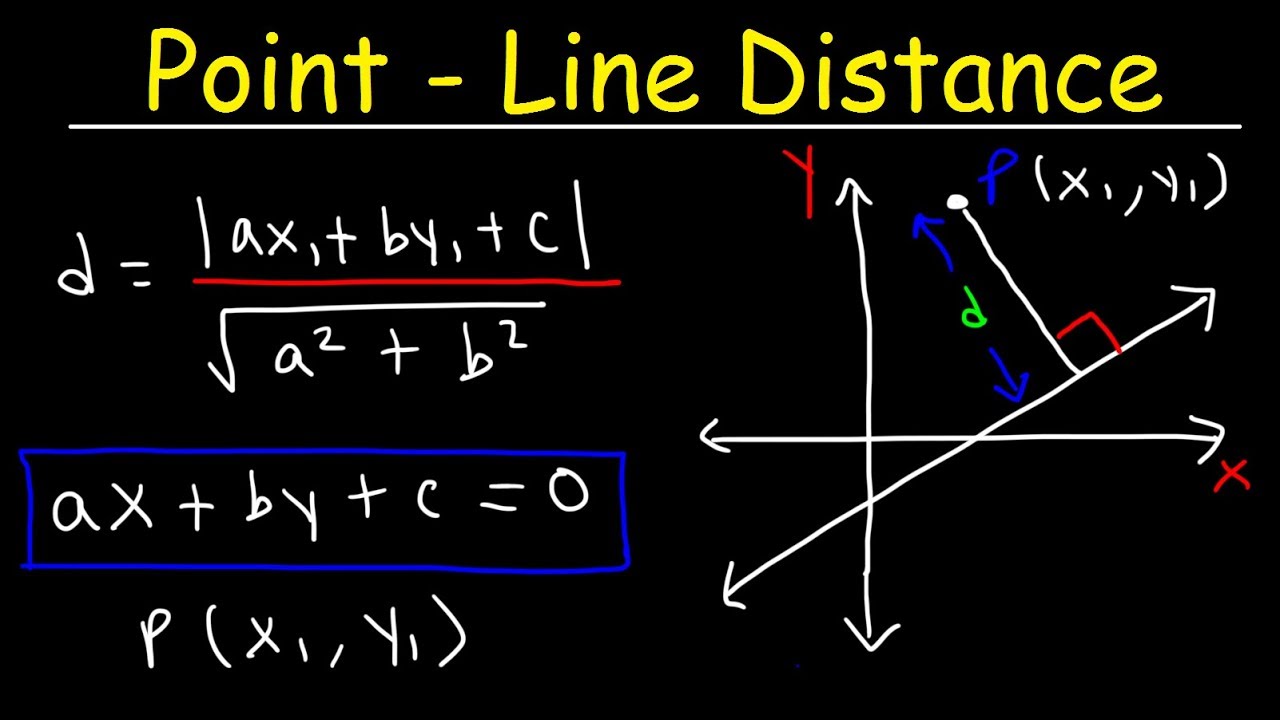
Ax + By + C = 0
Where A, B, and C are constants, and (x, y) are the coordinates of any point on the line. This equation can be rearranged to the slope-intercept form:
y = mx + b
Where m is the slope and b is the y-intercept. Understanding this representation is vital for calculating the distance from a point to the line.
Distance Formula from a Point to a Line
The formula for finding the distance (D) from a point (x0, y0) to a line represented by the equation Ax + By + C = 0 is given by:
D = (|Ax0 + By0 + C|) / √(A2 + B2)
This formula provides a straightforward method for calculating the perpendicular distance from the point to the line.
Practical Examples
Let’s examine a couple of examples to illustrate how to apply the distance formula effectively.
Example 1
Find the distance from the point (3, 4) to the line 2x + 3y - 6 = 0.
Here, A = 2, B = 3, C = -6, x0 = 3, and y0 = 4. Plugging these values into the formula:
D = (|2(3) + 3(4) - 6|) / √(22 + 32)
D = (|6 + 12 - 6|) / √(4 + 9)
D = (|12|) / √13
D ≈ 3.32 units.
Example 2
Find the distance from the point (1, -1) to the line x - 2y + 3 = 0.
Here, A = 1, B = -2, C = 3, x0 = 1, and y0 = -1. Using the formula:
D = (|1(1) - 2(-1) + 3|) / √(12 + (-2)2)
D = (|1 + 2 + 3|) / √(1 + 4)
D = (|6|) / √5
D ≈ 2.68 units.
Applications in the Real World
The concept of finding the distance from a point to a line has numerous applications in various fields:
- Engineering: Used in structural design and analysis.
- Computer Graphics: Important for rendering and collision detection.
- Urban Planning: Helps in determining the placement of roads and infrastructure.
- Physics: Utilized in trajectory calculations and motion analysis.
Common Mistakes in Calculating Distance
When calculating the distance from a point to a line, it’s easy to make some common mistakes. Here are a few to watch out for:
- Misidentifying the coefficients A, B, and C from the line equation.
- Forgetting to take the absolute value in the distance formula.
- Confusing the distance formula with the distance between two points.
Advanced Topics in Geometry
For those interested in furthering their knowledge, consider exploring the following advanced topics:
- Calculus and its application in finding distances in three-dimensional space.
- Vector analysis and its relevance to distance calculations.
- Geometric transformations and their effects on distances.
Conclusion
In conclusion, finding the distance from a point to a line is a crucial skill in mathematics and its applications. We have discussed the fundamental concepts, the mathematical representation of a line, and the distance formula. Additionally, we explored practical examples and real-world applications, emphasizing the importance of this knowledge in various fields.
We encourage you to practice these calculations and apply them in real-world scenarios. If you found this article helpful, please leave a comment and share your thoughts. Don't forget to check out our other articles for more insights!
Thank you for reading, and we look forward to seeing you again on our site!
Article Recommendations
- Tamron Halls Love Journey Exploring Her Past And Present Relationships
- Will Estes Wife The Life And Times Of A Private Partnership
- Liv Golf Results Payouts Latest Updates